NP 完全性的证明
引理：如果语言 $L$ 是一种满足对任意 $L’\in NPC$ 都有 $L’\le_{p}L$ 的语言，则 $L$ 是 NP-hardness。此外，如果 $L\in NP$，则 $L\in NPC$。
证明：
$\because L’\in NPC$
$\therefore$ 对于所有 $L’’\in NP$，都有 $L’’\le _{p}L’$
根据假设，$L’\le _{p}L$
$\therefore$ 根据传递性，$L’’\in _{p}L$
$\therefore$ $L$ 是 NP-hardness
那么，如果 $L\in NP$，且 $L$ 是 NP-hardness
$\therefore L\in NPC$
证明某种语言 $L$ 是 NP 完全问题的方法
- 证明 $L\in NP$
- 选取一种已知的 NP 完全语言 $L’$
- 描述一种可计算函数 $f(x)$ 的算法，其中 $f$可将 $L’$ 中每一个实例 $x\in \left{0,1\right}^*$ 映射为 $L$ 中的实例 $f(x)$
- 证明函数 $f$ 满足 $x\in L’$ 当前仅当对于所有的 $x\in \left{0,1\right}^*$ 都有 $f(x)\in L$
- 证明计算函数 $f(x)$ 的算法具有多项式运行时间
第 2 步 ~ 第 5 步是为了证明 $L$ 是 NP-hardness，然后结合第一步的 $L$ 是 NP 问题，就可以得出 $L\in NPC$。
典型 NPC 问题
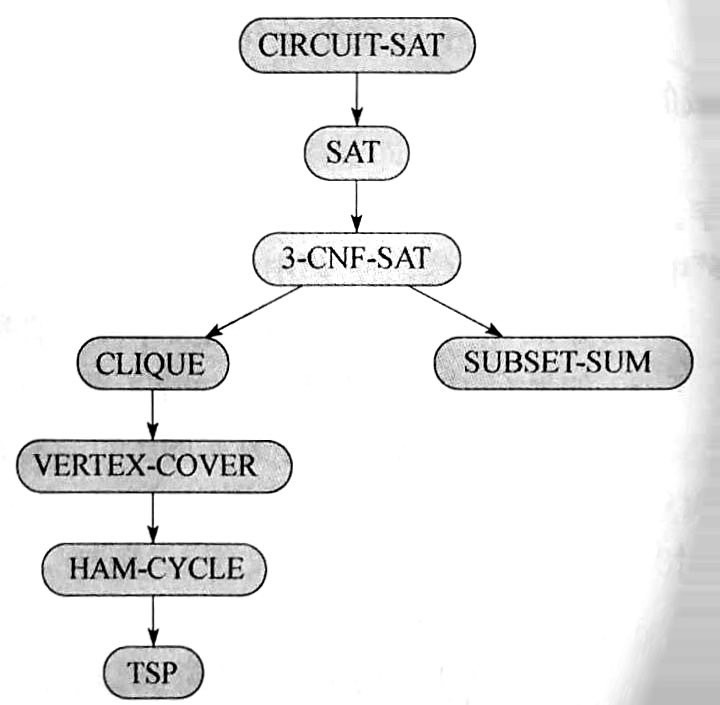一些典型的 NPC 问题
- SAT：布尔公式的可满足性问题
- 3-CNF-SAT：3 合取范式的布尔公式的可满足性问题
- 团问题 CLIQUE：寻找无向图中的最大团
- 顶点覆盖问题 VERTEX COVER：在无向图中找出最小规模的顶点覆盖
- 哈密顿回路问题 HAM-CYCLE：无向图中是否存在哈密顿回路，即通过每个顶点的简单回路
- 旅行商问题 TSP：寻找通过无向图每个顶点一次的最小回路
- 子集和问题 SUBSET-SUM：给定正整数集合和正整数 t，判断是否存在一个子集的元素和为 t
布尔组合电路
布尔组合电路由一个或多个布尔组合元素通过线路连接而成，布尔组合电路是不包括回路的。
一个布尔组合电路的真值赋值是指一组布尔输入值。如果一个单输出布尔组合电路具有可满足性赋值，则称该布尔组合电路是可满足的。
布尔值取自集合 $\left{0,1\right}$，0 代表 false，1 代表 true。
布尔组合元素称为逻辑门：$\begin{cases}与门\quad AND\或门\quad OR\非门\quad NOT\end{cases}$
For example：
- 对此电路的输入赋值 $<x_1=1, x_2=1, x_3=0>$，使得电路的输出为 1，那么电路是可满足的。
- 如果对此电路输入的任何一种赋值都不能使得输出为 1，则电路不满足。
NP 完全性证明
给定一个电路 C，通过检查输入的所有可能赋值来确定它是否来自可满足性电路。
那么，如果有 $k$ 个输入，就有检查 $2^k$ 种可能，因为$\begin{cases}1\0\end{cases}$
所以当电路 C 的规模为 $k$ 的多项式时，对每个电路的检查要花费 $\Omega(2^k)$ 的时间，呈多项式关系。
$\therefore$ 该问题是 NP 完全的
布尔可满足性问题 SAT
定理：布尔公式的可满足性问题是 NP 完全的。
证明：
- 证明 $SAT\in NP$，即证明对于输入公式 $\phi$，由它的一个可满足性赋值所组成的证书可以在多项式时间内得到验证
- 证明 $CIRCUIT-SAT\le _{p}SAT$ 从而得出 SAT 是 NP-hard
- 根据语言 $L\in NP$ 且 $L\in NP-hard$ 能推出 $L\in NPC$，得证
3-CNF 可满足性
即布尔公式中的一个文字（literal）是指一个变量或非 “$\neg$”。
合取范式
如果一个布尔公式可以表示为所有子句的“与”，并且每个字句都是一个或多个文字的“或”，则称该布尔公式为合取范式。
如果每个字句恰好有三个不同的“文字”，则该布尔公式为 3 合取范式，即 3-CNF。
For example：
合取范式
定理：3 合取范式形式的布尔公式的可满足性是 NP 完全的。
证明：要证明 $3-CNF-SAT\le NP$，仅需证明 $SAT\le _{p}3-CNF-SAT$。
团问题 CLIQUE
无向图 $G=(V,E)$ 的团 (clique) 是一个顶点子集 $V’\subseteq V$，其中每一对顶点之间都由 $E$ 中的一条边来连接。
一个团是 $G$ 中的一个完全子图，图的规模是指它所包含的顶点数。
团问题就是关于寻找图中规模最大的团的优化问题。
事实上，团问题的有效算法是不大可能存在的。因为要确定一个具有 $|V|$ 个顶点的无向图 $G=(V,E)$ 是否包含一个规模为 $k$ 的团，有一种朴素算法：
列出V的所有规模为 $k$ 的子集，对其中的每一个进行检查，看它是否是一个团。这个算法的运行时间是与 $k$ 有关。如果 $k$ 是常数，那么该算法的运行时间是多项式时间的。然而，在一般情况下，$k$ 可能接近于 $|V|/2$。这样的话，运行时间就是超多项式时间。所以，团问题的有效算法是不大可能存在的。
形式语言定义
$CLIQUE=\left{<G,k>:G是一个包含规模为k的团的图\right}$
定理：$CLIQUE\subseteq NP-Complete$
证明：首先，证明 $CLIQUE\in NP$。然后，证明 $CLIQUE\in NP-hard$
- 对于一个给定的图 $G=(V,E)$，用图中顶点集 $V’\subseteq V$ 作为 $G$ 的一个证书。对于任意一对顶点 $\mu,\nu\in V’$，通过检查边 $(\mu,\nu)$ 是否属于 $E$，就可以在多项式时间内确定 $V’$ 是否是团。
- 通过证明 $3-CNF-SAT\le _{p}CLIQUE$ 来说明 $CLIQUE\in NP-hard$。
顶点覆盖问题 Vertex Cover
无向图 $G=(V,E)$ 的顶点覆盖是一个子集 $V’\subseteq V$，满足如果有 $(\mu,\nu)\in E$，则 $\mu\in V’$ 或 $\nu\in V’$（或两者同时成立）。
顶点覆盖的规模是指它所包含的顶点数。顶点覆盖问题就是在一个给定的图中，找出具有最小规模的顶点覆盖。
形式语言定义
$VERTEX-COVER=\left{<G,k>:图G有一个规模为k的顶点覆盖\right}$
定理：$VC\subseteq NP-Complete$
证明：首先，证明 $VC\in NP$。然后证明 $CLIQUE\le _{p}VC$ 从而得到 $VC\in NP-hard$
哈密顿回路问题 HAM-CYCLE
定理：哈密顿回路问题是 NP-Complete
证明：首先，证明 $HAM-CYCLE\in NP$。然后通过证明 $VC\le _{p}HAM-CYCLE$ 从而得到 $HAM-CYCLE\in NP-hard$
旅行商问题 TSP
形式语言定义
$$TSP=\left{<G,c,k>:G=(V,E)是一个完全图，c是V*V\rightarrow Z上的一个函数，k\in Z，G中包含一个最大花费为k的旅行回路。\right}$$
定理：旅行商问题是 NP-Complete
证明：首先，证明 $TSP\in NP$。然后通过证明 $HAM-CYCLE\le _{p}TSP$ 从而得到 $TSP\in NP-hard$
子集和问题 SUBSET-SUM problem
给定一个正整数有限集 $S$ 和一个整数目标 $t>0$，问是否存在一个子集 $S’\subseteq S$，其元素和为 $t$。
形式语言定义
$SUBSET-SUM=\left{<S,t>:存在一个子集S’\subseteq S，使得t= \sum\limits_{S\in S’}S\right}$
定理：子集和问题是 NP-Complete
证明：首先，证明 $SUBSET-SUM\in NP$。然后，通过证明 $3-CNF-SAT\le _{p}SUBSET-SUM$ 从而得到 $SUBSET-SUM\in NP-hard$