马尔可夫性
某一状态信息包含了相关的历史，只要当前状态可知，所有的历史信息都不再需要，当前状态就可以决定未来，则认为该状态具有马尔可夫性（Markov Property）。
马尔可夫性
马尔可夫过程
又叫马尔可夫链（Markov Chain）。它是一个无记忆的随机过程，可以用一个元组 $<S, P>$ 表示，其中 $S$ 是有限数量的状态集，$P$ 是状态转移概率矩阵。
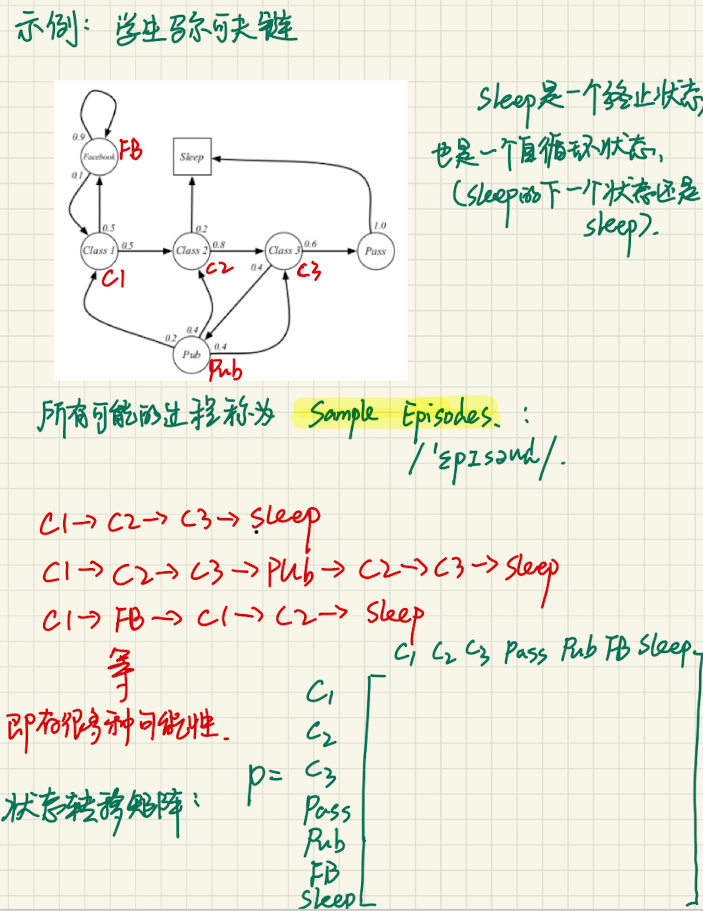马尔可夫过程
马尔可夫奖励过程
马尔可夫奖励过程（Markov Reward Process）在马尔可夫过程的基础上增加了奖励R和衰减系数V：$<S, P, R, V>$。$R$ 是一个奖励函数。$S$ 状态下的奖励是某一时刻 $(t)$ 处所在状态 $s$ 下在下一个时刻 $(t+1)$ 能获得的奖励期望：
$$
R_s = E[R_{t+1}|S_t=s]
$$
衰减系数（Discount Factor）：$\gamma\in[0, 1]$，避免无限循环。
马尔可夫决策过程
Markov Decision Process，MDP
多了一个行为集合 $A$，元组 $<S, A, P, R, V>$。
$$
P^a_{ss’} = P[S_{t+1}=s’|S_t=s, A_t=a]
$$
$$
R^a_s=E[R_{t+1}|S_t=s, A=a]
$$
当给定一个 MDP： $<S, R, P,R, \gamma>$ 和一个策略 $\pi$，那么状态序列 $S_1，S_2$，是一个马尔可夫过程 $<S, P^\pi>$。
下一个时刻的状态 $S_{t+1}$ 和当前时刻的状态 $S_t$ 以及动作 $a_t$ 有关。
过程
$$
初始化状态agent所处状态s_0
$$
$$
\Downarrow
$$
$$
根据policy\quad\pi(a|s)采取动作a_0，a_0\sim\pi(a|s_0)
$$
$$
\Downarrow
$$
$$
根据转移概率p(s’|s,a)采取新状态s_1，s_1\sim p(s’|s,a)
$$
$$
\Downarrow
$$
$$
得到单步奖励r_1=R^{a_0}{s_0s_1}
$$
$$
\Downarrow
$$
$$
持续，得到终止状态S_T，得到轨迹\gamma=(s_0,a_0,s_1,a_1,\dots,s_T)
$$
$$
\Downarrow
$$
$$
轨迹的联合概率：
$$
$$
p(r)=p(S_0)·\prod^\pi{t=1}p(a_{t-1}|S_{t-1})·p(S_t|S_{t-1},a_{t-1})
$$
$$
\Downarrow
$$
$$
对于每一条轨迹，累计奖励函数是关于单步奖励的函数
$$
$$
R=f(r_0,r_1\dots r_{T-1})
$$
$$
\downarrow
$$
$$
可以是T步累计奖励函数R=\sum^{T-1}{t=0}r_t，
$$
$$
也可以是\gamma折扣奖励函数，R=\sum^{T-1}{t=0}\gamma^t·r_t
$$
$$
\Downarrow
$$
$$
期望累计奖励是E_R=E_p(r)[\sum^{T-1}{t=0}\gamma^t·r_t^T]
$$
$$
\therefore agent的目标策略就是使得期望累计奖励最大的策略
$$
$$
\pi=\max\limits{\pi}E_{p(r)}^\pi[\sum^{T-1}_{t=0}\gamma^t·r_t]
$$
状态 state
agent 在每个步骤中所处于的状态集合。
行为 action
agent 在每个步骤中所能执行的动作集合。
转移概率 transition
agent 处于状态 $s$ 下，执行动作 $a$ 后，会转移到状态 $s’$ 的概率。
奖励 reward
agent 处于状态 $s$ 下，执行动作 $a$ 后，转移到状态 $s’$ 后获得的立即奖励值。
策略 Policy
策略 $\pi$ 是概率的集合或分布，其元素 $\pi(a|s)$ 为对过程中的某一状态 $s$ 采取可能的行为 $a$ 的概率。
agent 处于状态 $s$ 下，应执行动作 $a$ 的概率。
一个策略定义了个体在各个状态下的各种可能的行为方式以及其概率的大小。
回报 Return
回报 $G_t$ 为在一个马尔可夫奖励链上从 $t$ 时刻开始往后所有的奖励的有衰减的总和。
价值函数 Value Function
价值函数给出了某一状态或某一行为的长期价值。
某一状态的价值函数为从该状态开始的马尔可夫链收获的期望。
Bellman Optimality Equation
针对 $V*$，一个状态的最优价值等于从该状态出发采取的所有行为产生的行为价值中最大的那个行为价值：
$$
V_*(s)=\max_aq_*(s,a)
$$
值函数
状态值函数 State Value Function
$V^\pi(s)$ 为状态值函数，表示从状态 $s$ 开始，执行策略 $\pi$ 得到的期望总回报：
$$
V^\pi(s)=E_{r\sim p(r)}[\sum^{T-1}{t=0}\gamma^t·r{t+1}|\tau_{s_0}=s]
$$
其中 $\tau_{s_0}$ 表示轨迹 $\gamma$ 的起始状态。
$$
V^\pi(s)=E_{a\sim\pi}(a|s)E_{s’\sim p(s’|s,a)}[r(s,a,s’)+\gamma V^\pi(s’)]
$$
$$
\downarrow
$$
Bellman equation，表示当前状态的值函数可以通过下个状态的值函数来计算。
状态——动作值函数
也叫 Q 函数，Q-function。指初始状态为 $s$ 并进行动作 $a$，然后执行策略 $\pi$ 得到的期望总回报，即 state-action value function。
$$
Q^\pi(s,a)=E_{s’\sim p(s’|s,a)}[r(s,a,s’)+\gamma·V^\pi(s’)]
$$
也可以写成：
$$
Q^\pi(s,a)=E_{s’\sim p(s’|s,a)}[r(s,a,s’)+\gamma·E_{a’\sim\pi(a’|s’)}[Q^\pi(s’,a’)]]
$$
$$
\uparrow
$$
$$
Q 函数的 Bellman 方程
$$
基于值函数的策略学习方法
主要分为动态规划和蒙特卡罗。
动态规划
动态规划又分为策略迭代（policy iteration）算法和值迭代（value iteration）算法。
策略迭代
策略评估 policy evaluation
计算当前策略下，每个状态的值函数。可以通过 Bellman 方程进行迭代计算$V^\pi(s)$。
策略改进 policy improvement
根据值函数更新策略。
值迭代
将策略评估与策略改进合并，来直接计算出最优策略。
策略迭代 vs 值迭代
蒙特卡罗
Q 函数。$Q^\pi(s,a)$ 为初始状态为 $s$，并执行动作 $a$ 后所能得到的期望总回报。
$$
Q^\pi(s,a)=E_{r\sim p(r)}[G(\tau_{s_0}=s,a_0=a)]
$$
$\tau_{s_0}=s，a_0=a$ 表示轨迹 $\tau$ 的起始状态和动作为$s$，$a$。
蒙特卡罗方法
Q 函数通过采样进行计算。
对于一个策略 $\pi$，agent 从状态 $s$，执行动作 $a$ 开始，然后通过随机游走的方法探索环境，并计算其总回报。
在得到 Q 函数 $Q^\pi(s,a)$ 之后，进行策略改进，在新策略下采样估计 Q 函数，不断重复。
$\epsilon$-贪心法
$$
\pi^\epsilon=\begin{cases}
\pi(s),按概率1-\epsilon\
随机选择\mathcal{A}中的动作，按概率\epsilon
\end{cases}
$$
将一个仅利用的策略转为带探索的策略，每次选择动作 $\pi(s)$ 的概率为 $1-\epsilon+\frac{1}{|\mathcal{A}|}$，其它动作的概率为 $\frac{1}{\mathcal{A}}$。
同策略与异策略
时序差分学习方法
蒙特卡罗采样方法一般需要拿到完整的轨迹，才能对策略进行评估并更新模型，因此效率较低。
时序差分学习（temporal-difference learning）结合了动态规划和蒙特卡罗方法：模拟一段轨迹，每行动一步（或几步）就利用 Bellman 方程来评估行动前状态的值。（当每次更新动作数为最大数时，就等价于蒙特卡罗方法）。
SARSA 算法
State Action Reward State Action
只需要知道当前状态 $s$ 和动作 $a$，奖励 $r(s,a,s’)$，下一步的状态 $s’$ 和动作 $a’$，其采样和优化的策略都是 $\pi^\epsilon$，因此是同策略。
$$
Q^\pi(s,a)\longleftarrow Q^\pi(s,a)+\alpha(r(s,a,s’)+rQ^\pi(s’,a’)-Q^\pi(s,a))
$$
SARSA 算法
Q 学习算法
Q-learning
$$
Q(s,a)\longleftarrow Q(s,a)+\alpha(r+\gamma\max_{a’}Q(s’,a’)-Q(s,a))
$$
Q-learning 算法
与 SARSA 不同，Q-learning 不通过 $\pi^\epsilon$ 来选下一步的动作 $a’$，而是直接选最优的 Q 函数。更新后的 Q 函数是关于策略 $\pi$ 的，而不是策略 $\pi^\epsilon$ 的。