二分图定义
可以把图中的点分成两部分,使得每部分内部两两点之间没有连边。
判定是否是二分图
没有奇数环的图,或者能够黑白染色(染色问题)的图。
完美匹配
定义
一个图的最大匹配中的每个点都是匹配点
Hall 定理
设 $G$ 是具有二划分 $(X, Y)$ 的二部图,则G有饱和X的匹配当且仅当对 $∀S ⊆ X , N ( S ) ≥ |S|$,其中 $N(S)$ 表示 $S$ 的所有邻点之集。
通俗的说,即**选择任意的左部点 $S$ 个,把所有这 $S$ 个点关联的 $K$ 个右部点取出来,一定有 $|S|<=|K|$**。如果满足这个条件,则是二分图。
Tutte 定理
A graph, G = (V, E), has a perfect matching if and only if for every subset U of V, the subgraph induced by V − U has at most |U| connected components with an odd number of vertices.
图 $G$ 有完美匹配的充分必要条件是**对 $∀S ⊂ V (G) , O (G \setminus S ) ≤| S |$**。
即图 $G$ 有完美匹配等价于,对于图 $G$ 去掉任意一个点集之后,图的奇分支的个数小于等于点集的个数(奇分支:有奇数个点的分支)。
例如,对于下图,证明其是否有完美匹配。
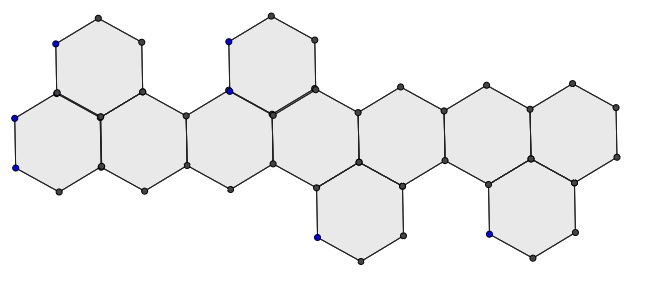
可以在图中挑出一些点,使得点与点之间分隔后的部分有奇数个顶点,然后比较挑出的点的数量,与分隔后的部分的数量的大小。如果分隔后部分的数量小于等于挑出点的数量,则有完美匹配。
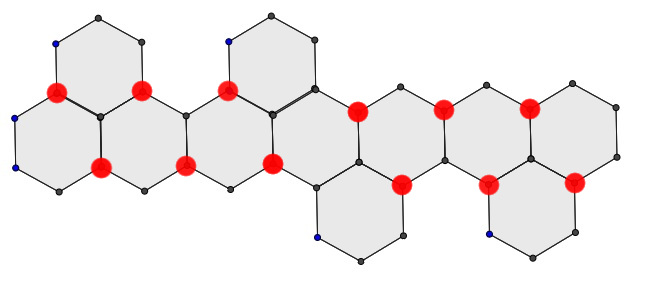
如上图所示,挑出 12 个红点,这 12 个红点将图分成了 14 个部分(每个部分必须含有奇数个顶点)。因为 12 < 14,不满足 Tutte 定理,所以这个图没有完美匹配。